Pengertian Pertidaksamaan Nilai Mutlak, Sifat, Rumus, Jenis, Contoh Soal dan Penyelesaiannya. Inilah penjelasan materi pertidaksamaan nilai mutlak lengkap dengan materi penunjang seperti rumus pertidaksamaan, sifat dan jenisnya. Tidak lupa akan rumuspelajaran.com sampaikan pengertian umum pertidaksamaan dalam matematikanya. Banyak juga yang mencari contoh soal dan jawaban pertidaksamaan ketika mendapati soal maupun tugas sekolah.

Pertidaksamaan linear ini bisa diartikan secara singkat sebuah materi matematikan yang berisikan perbandingan dan untuk penjelasannya bisa sobat baca di artiel ini. Ada beberapa sifat pertidaksamaan yang mungkin perlu dipelajari sobat ketika menginjak materi ini di sekolah. Bagian terpenting dari artiel ini yaitu yang sering dicari adalah tentang rumus pertidaksamaannya, walaupun sifat dan jenis pertidaksamaan juga sama pentingnya.

Perlu sobat ketahui jika pada kesempatan lainya tim RUMUS PELAJARAN telah memposting materi simpangan baku lengkap pengertian, rumus, perhitungan, fungsi, contoh-contoh soalnya dan materi Trigonometri kelas 11, apa itu kuadran dan lengkap dengan sejarahnya. Inilah penjelasan apa tiu pertidaksamaan linear satu variable dan penjelasan lainya seperti jenis, sifat, contoh soal dan rumus pertidasamaannya dibawah ini.

Pengertian Pertidaksamaan Linear Satu Variabel

Pengertian umum pertidaksamaan dalam matematika merupakan kalimat/pernyataan matematika yang menunjukkan perbandingan ukuran dua objek atau lebih. Dua notasi dasar dalam pertidaksamaan dapat sobat lihat dalam tabel berikut ini:

Atau bisa diartikan sebagai kalimat terbuka yang menggunakan tanda ketidaksamaan (<, >, ≤, ≥) dan mengandung variakel. Secara umum pertidaksamaan merupakan cara untuk menyatakan suatu selang atau interval.

Tanda “<” dan “>” menyatakan selang terbuka dan pada garis bilangan digambarkan dengan noktah kosong( ). Kemudian Pertidaksamaan nilai mutlak merupakan jenis pertidaksamaan yang mengandung nilai mutlak. Nilai mutlak menghitung jarak suatu angka dari 0—misal, x. mengukur jarak x dari nol.

Persamaan nilai mutlak merupakan sebuah persamaan yang selalu bernilai positif.Pertidaksamaan nilai mutlak ialah sebuah perbandingan ukuran dua objek atau lebih yang selalu bernilai positif.

Sifat Pertidaksamaan Nilai Mutlak

Untuk dapat mengambil nilai mutlak dari suatu persamaan nilai mutlak sebenarnya cukup mudah. Cukup mengikuti 2 aturan penting sehingga sobat mampu dapat menentukan nilai mutlaknya. Jadi, nilainya akan positif jika fungsi di dalam tanda mutlak lebih dari nol. Dan akan bernilai negatif kalau fungsi di dalam tanda mutlak kurang dari nol.

Sebenarnya ada beberapa pertidaksamaan aljabar yang ekuivalen dengan pertidaksamaan nilai mutlak dan nilai mutlak tidak cukup dengan cara tersebut. Ataupun dapat disebut saja sebagai sifat pertidaksamaan nilai mutlak.

Selanjutnya akan kita simak sifat-sifat pertidaksamaan nilai mutlak adalah sebagai berikut :

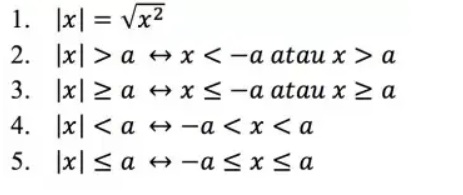
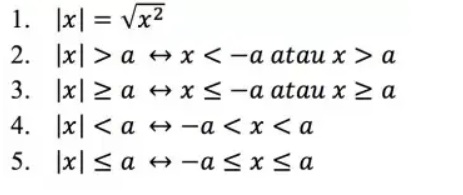
Itulah cara dasar dalam mengoperasikan suatu bilangan dan variabel.

Rumus Pertidaksamaan Nilai Mutlak

Mungkin sudah banyak yang penasaran bagaimana rumus dari pertidaksamaan mutlak ini, ketika nilai mutlak suatu bilangan real x ialah jarak antara bilangan itu dengan nol pada garis bilangan. Dan digambarkan dengan │x│. Secara formal nilai mutlak didefinisikan dibawah ini :

Pengantar Nilai Mutlak

Perlu diketahui sobat pelajar jika fungsi utama nilai mutlak merupakan fungsi yang kontinu. Jika kita gambarkan dalam bentuk grafik, gambar grafik fungsi nilai mutlak membentuk garis lurus, seperti membentuk huruf v pada interval tertentu.

Grafik yang dihasilkan memiliki satu buah titik puncak dan garisnya simetris, antara ruas kanan dan kiri.

Lihatlah gambar grafik nilai mutlak yang diberikan seperti gambar berikut ini.

Contoh Soal Pertidaksamaan Linear Satu Variabel (PtLSV) Dan Cara Penyelesaiannya

Berikut ini merupakan contoh soal dan cara penyeleaiannya dan juga jawaban dari pertidaksamaan linear satu variabel.

1. Penjumlahan dan Pengurangan

Silakan perhatikan pertidaksamaan dibawah ini :

x + 3 < 8, dengan x variabel dari bilangan bulat.

Untuk:

x = 1, jadi 1 + 3 < 8, bernilai benar
x = 2, jadi 2 + 3 < 8, bernilai benar
x = 3, jadi 3 + 3 < 8, bernilai benar
x = 4, jadi 4 + 3 < 8, bernilai salah

Pengganti x adalah 1,2, dan 3 sehingga pertidaksamaan x + 3 < 8 adalah benar dinamakan penyelesaian dari pertidaksamaan tersebut. Gambar soal Tentukanlah penyelesaian dari 4x > 3x – 5, untuk:

2. Perkalian atau pembagian

Lihatlah pertidaksamaan dibawah ini:

contoh soal pertidaksamaan linear satu variabel

Untuk bilangan x asli kurang dari 10 maka penyelesaiannya yaitu x = 7, x = 8, atau x = 9

Berdasarkan uraian diatas, dapat diambil kesimpulan bahwa:

Perlu dicatat jika Setiap pertidaksamaan tetap ekuivalen, dengan tanda ketidaksamaan tidak berubah, meskipun kedua ruas dikalikan dengan bilangan positif yang sama.

Contoh Soal:

1. –x > – 5, dengan x merupakan bilangan asli kurang dari 8. Pengganti x yang memenuhi adalah x = 1, x = 2, x = 3 atau x = 4.

Jawaban:

* –x > –5

–1(–x) > – 1(–5), (kedua ruas dikalikan dengan –1 serta tanda pertidaksamaan tetap)

x > 5

Penyelesaiannya adalah x = 6 atau x = 7.

* –x > –5

–1(–x) < –1(–5), (kedua ruas dikalikan dengan –1 dan tanda pertidaksamaan berubah dari > menjadi <)

x < 5 Penyelesaiannya adalah x = 1, x = 2, x = 3, atau x = 4. Berdasarkan penyelesaian tersebut ternyata, pertidaksamaan yang memiliki penyelesaian sama yaitu –x > –5 dan –1(–x) < –1(–5) sehingga, –x > –5 <=> –1(–x) < –1(–5)

2. –4x <–8, dengan x bilangan asli kurang dari 4. Pengganti x yang memenuhi adalah x = 2, atau x = 3. sehingga, penyelesaiannya adalah x = 2 atau x = 3.

Berdasarkan penjelasan diatas dapat diambil kesimpulan bahwa:

“Suatu pertidaksamaan apabila kedua ruasnya dikalikan dengan bilangan negatif yang sama maka tanda pertidaksamaan berubah”

Contoh Soal dan Jawaban:

Pelajari Juga:

• Pengertian Persegi, Sifat, Macam, Definisi, Rumus, Luas, Keliling, Unsur dan Contoh Soal
• Pengertian Lensa Cembung, Rumus, Sifat, Jenis dan Sinar Istimewa
• Pengertian Future Perfect Tense, Rumus, Macam, Fungsi dan Contoh Kalimat

Demikianlah materi Materi Pertidaksamaan Nilai Mutlak, Sifat, Rumus, Jenis, Contoh Soal dan Penyelesaiannya, semoga bisa menambah pengetahuan dalam pelajaran Matematika khususnya.