Pengertian Relasi, Fungsi, Perbedaan, dan Contoh Soal. Materi tentang Apa itu relasi dan apa definisi dari fungsi dalam mata pelajatan matematika. Materi pelajaran matematikan kelas 8 (delapan) ini memang menarik dan diajarkan kepada siswa maupun siswi SMP. Cara mudah untuk mengerjakan soal relasi dan fungsi serta perbadaanya tentunya wajib mengetahui materi ini sejak dari awal. Di dalam materi yang akan di sampaikan laman pendidikan rumuspelajaran.com ini membahas juga mengenai perbedaan relasi dan apa itu fungsi, dan tentunya akan disertakan beberapa contoh gambar relasi maupun fungsi itu sendiri.

Rangkuman materi pengertian relasi dan fungsi ini wajib sobat pelajar catat supaya lebih mudah dalam mempelajari dan memahaminya. Untuk belajar sekarang bisa lebih mudah karena bisa menggunakan smartphone ataupun laptop sebagai media penyimpanan materi. Mungkin sobat juga mencari materi matematika yang berkaitan dengan cara mengubah pecahan desimal menjadi pecahan biasa, cara menghitung besar salah satu sudut segitiga yang belum diketahui maupun rumus matematika SMP.

Pada kesempatan sebelumnya laman pendidikan RP (rumuspelajaran.com) telah membahas mengenai pengertian simpangan baku lengkap rumus, perhitungan, fungsi dan contoh-contoh soalnya serta materi trigonometri lengkap dengan sejarah, fungsi dan rumus trigonometri. Baiklah sekarang langsung saja ke pokok pembahasan materi kali ini yang diawali dengan membahas mengenai apa itu Relasi, Fungsi dan beberapa contoh gambarnya.

Pengertian Relasi dan Fungsi

Apa itu definisi relasi dan bagaimana sifat-sifat fungsi, nah kali ini sobat akan menambah ilmu pengetahuan matematikanya yang membahas mengenai seperti prolog diatas. Dalam pelajaran matematika relasi ini berkaitan erat dengan apa itu daerah asal, hasil dan kawan beserta penjelasan lainya. Simak sampai selesai materi in karena sering muncul dalam soal fungsi kelas 8 kurikulum 2013, biasanya.

Relasi

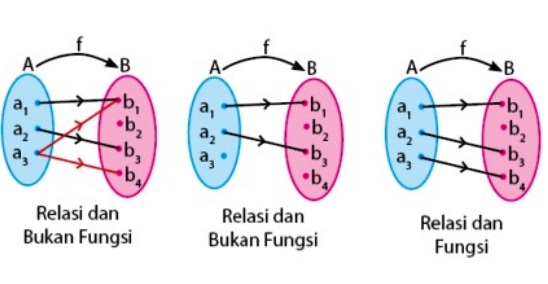
Penjelasan tentang Relasi merupakan suatu hubungan. Nah, hubungan di sini yang dimaksud adalah hubungan antara daerah asal (domain) dan daerah kawan (kodomain). Sedangkan fungsi merupakan relasi yang memasangkan setiap anggota himpunan daerah asal tepat satu ke himpunan daerah kawannya. Perbedaan antara relasi dan fungsi terletak pada cara memasangkan anggota himpunan ke daerah asalnya.

Pada relasi ini yang perlu diperhatikan yaitu ternyata mempunyai aturan khusus ketika memasangkan setiap anggota himpunan daerah asal ke daerah kawan yang bertempatan di sampingnya. Aturan ini memang hanya terikat atas pernyataan relasi tersebut.

Ketika anggota himpunan daerah asal boleh mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan. Kemudian jika fungsi, setiap anggota himpunan daerah asal dipasangkan dengan aturan khusus. Aturan ini mengharuskan setiap anggota himpunan daerah asal mempunyai pasangan dan hanya tepat satu dipasangkan dengan daerah kawannya.

Jadi kesimpulanya setiap relasi belum tentu fungsi, namun setiap fungsi pasti merupakan relasi. Itulah penjelasan singkatnya mengenai relasi dan fungsi yang menjadi prolog dan topik di pembahasan awal. Untuk memperdalam materi kali ini kita akan lanjutkan relasi dan fungsi melalui ulasan lebih lengkapnya dibawah ini.

Daerah Asal, Kawan, dan Hasil

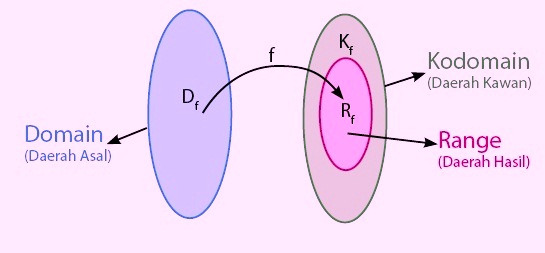
Diatas telah dibawah mengenai relasi dan fungsi, himpunan yang terlibat digolongkan ke dalam tiga jenis daerah. Ketika ketiga daerah tersebut adalah daerah asal (domain), daerah kawan (kodomain), dan daerah hasil (range). Bisa disimpulkan ketika himpunan ketiga daerah tersebut dapat dilihat pada gambar yang telah disiapkan laman pendidikan rumuspelajaran.com dibawah ini.

Penjelasan mengenai ketiga daerah tersebut bisa dijelaskan dibawah ini.

• Domain atau daerah asal adalah himpunan tidak kosong di mana anggota sebuah relasi didefinisikan.
• Kodomain adalah atau daerah kawan merupakan himpunan tidak kosong dimana anggota domain memiliki pasangan sesuai relasi yang didefinisikan.
• Range atau daerah hasil adalah semua anggota kodomain yang memiliki pasangan pada anggota domain.

Berikut ini cara menyatakan hasil relasi perkalian antara himpunan A dan B dengan mudah dan cepat.

A = { 1, 2, 3 }
B = { 2, 3 }
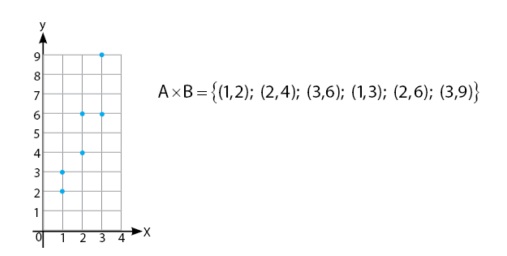
A × B = {1, 4, 6, 3, 6, 9}

Ketika relasi menyatakan pemetaan dengan fungsi f(x) adalah perkalian A dan B. Dan anggota himpunan x merupakan semua anggota A dan anggota himpunan y atau f(x) ialah hasil perkalian anggota A dan B.

x = {1, 2, 3}
y = {1, 4, 6, 3, 6, 9}

Gambar Bidang Kartesius

Fungsi atau Pemetaan

Arti fungsi atau pemetaan juga termasuk dalam relasi. Suatu relasi disebut fungsi jika semua anggota himpunan daerah asal dipasangkan tepat satu ke daerah kawannya.

Simbol fungsi memetakan himpunan A ke B yaitu:

f : A → B

Contoh permasalahan pada fungsi :

A = { 0, 1, 2, 3, 4 }
B = { 0, 1, 2, …, 10}

Didefinisikan fungsi f : A → B dengan f(x) = x + 5.

Contoh soal:

Tentukan hasil pemetaan dari x ∈ A oleh fungsi f, Df, Kf, dan Rf!

Pembahasan:

Peta dari x ∈ A oleh fungsi f yaitu y = f(x) = x + 5:

f(0) = 0 + 5 = 5
f(1) = 1 + 5 = 6
f(2) = 2 + 5 = 7
f(3) = 3 + 5 = 8
f(4) = 4 + 5 = 9

Pelajari juga:

• Pengertian Tenaga Nuklir, Sejarah, Jenis, Manfaat, Keuntungan dan Contoh
• Apa itu Cermin Cembung, Rumus, Sifat, Sinar Istimewa, Fungsi, Efek, Sifat Bayangan dan Contoh Soal

Hasilnya dari perhitungan f(x) hasil/range, daerah asal/domain merupakan semua anggota himpunan A. Sedangkan daerah kawan/kodomain adalah semua anggota B.

Daerah asal (domain): Df = A = { 0, 1, 2, 3, 4 }
Daerah kawan (kodomain): Kf = B = { 0, 1, 2, …, 10}
Daerah hasil (range) = Rf = {5, 6, 7, 8, 9}

Sifat-sifat Fungsi

Berikut ini yang bisa sobat pelajari mengenai 3 sifat fungsi yang terbagi menjadi 3 (tiga) jenis yaitu fungsi Injektif, Surjektif, dan Bijektif yang penjelasanya bisa kita simak dibawah ini dan pengelompokkan tersebut didasarkan pada sifatnya.

1. Fungsi Injektif

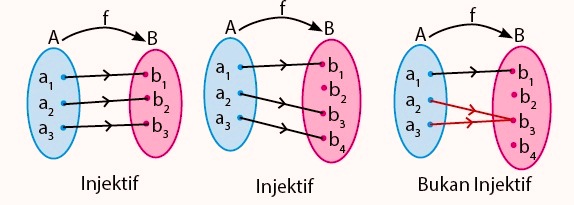
Fungsi injektif atau disebut juga dengan fungsi into atau fungsi satu-satu.

Fungsi f : A → B dikatakan fungsi injektif jika dan hanya jika anggota kodomain hanya dipasangkan satu kali dengan anggota domain.

Pada fungsi injektif, anggota himpunan daerah kodomain boleh tidak memiliki pasangan, namun semua anggota kodomain yang terpasangkan hanya ada satu, tidak boleh ada yang lebih dari satu.

2. Fungsi Surjektif (Fungsi Onto)

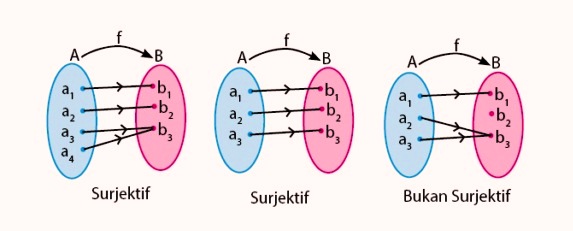
Fungsi Surjektif atau onto mempunyai ciri sebagai anggota kodomainnya boleh memiliki pasangan lebih dari satu, namun tidak boleh ada anggota kodomain yang tidak dipasangkan. Fungsi surjektif ini adalah memenuhi jumlah anggota kodomain sama atau lebih sedikit dari anggota domain.

3. Fungsi Bijektif (Korespondensi Satu-Satu)

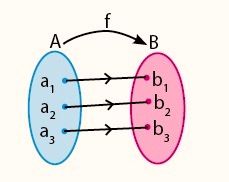
Fungsi Bijektif adalah gabungan dari fungsi injektif dan surjektif. Pada fungsi bijektif, semua anggota domain dan kodomain terpasangkan tepat satu.

Kebalikan dari fungsi dari fungsi injektif dan surjektif belum pasti fungsi/pemetaan, namun kebalikan fungsi dari fungsi bijektif juga merupakan fungsi/pemetaan.

Lihat materi lain seperti RUMUS LENSA CEKUNG DAN APA ITU TEKS EDITORIAL.

Demikianlah materi pembahasan kali ini yang mempelajari mengenai apa itu Relasi, sifat-sifat Fungsi dan juga perbedaanya. Semoga dengan adanya tambahan ilmu ini menamabah semangat belajat sobat rumuspelajaran.com semua ya.